Angewandte Mathematik in den Naturwissenschaften

Forschung

SFB 1456 Mathematik des Experiments

  • Projekt B06: Compensating motion and model inexactness in nano-CT and local tomography (mit Tim Salditt)
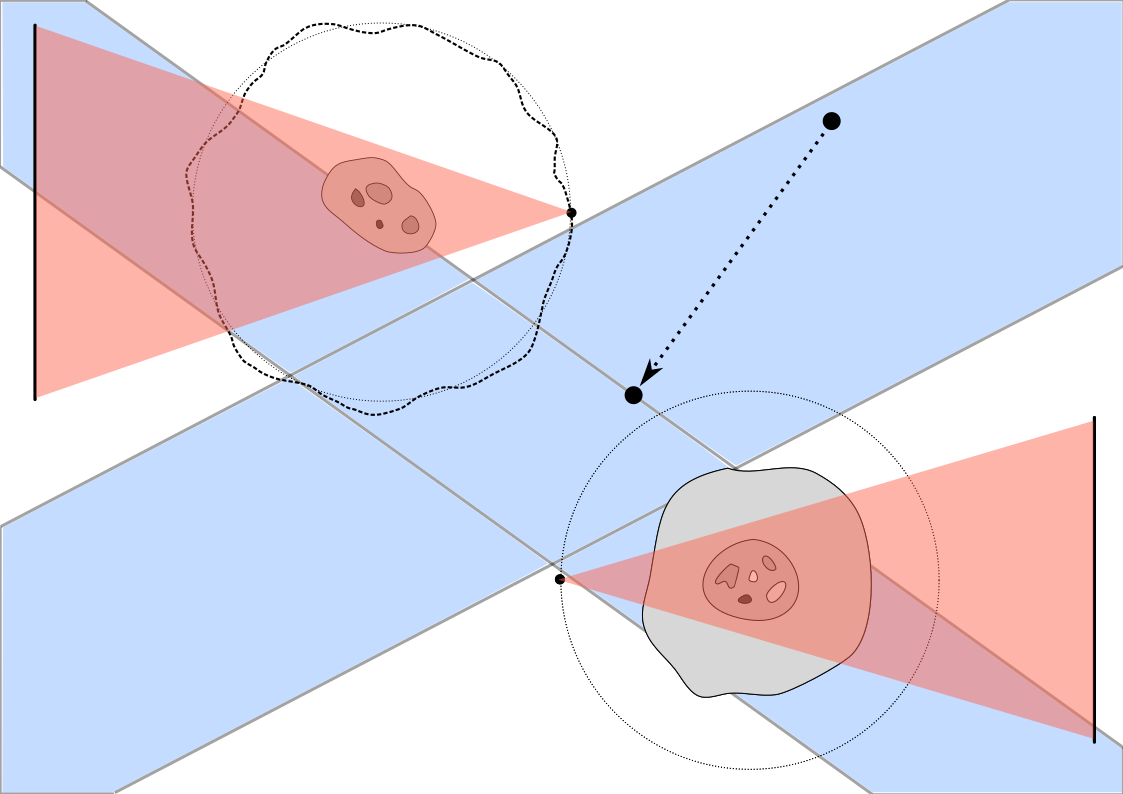
Image B06

Bei der tomografischen Bildgebung mit Röntgenstrahlen im Nanobereich müssen mehrere Hürden überwunden werden, z. B. die Relativbewegung zwischen dem Scanner und dem Objekt sowie das Vorhandensein von unbekanntem Material außerhalb des Zielbereichs. In diesem Projekt zielen wir darauf ab, vereinfachte mathematische Modelle zu verwenden und Strategien zu entwickeln, um die daraus resultierenden Modellierungsfehler mit Hilfe analytischer, statistischer und datengesteuerter Techniken zu kompensieren, um effiziente und präzise Bildgebungsalgorithmen zu erhalten, die speziell für die Nano-CT-Bildgebung geeignet sind.

GRK 2756 Cytoskeletal elements of active matter – from molecular interactions to cellular biophysics (CYTAC)

  • Projekt A4: Multiscale rheological inverse problems and active processes in cells
Image A4

Die Bestimmung mechanischer Eigenschaften von aktiver Materie, wie beispielsweise die Viskosität, erfordert üblicherweise die Auswertung indirekter Messdaten, da die entsprechenden Parameter nicht direkt gemessen werden können. Mathematisch handelt es sich also um ein inverses Problem: Eine unbekannte Größe soll aus ihrer Auswirkung auf eine messbare Größe bestimmt werden, wobei die Messungen oft rauschbehaftet sind. In diesem Projekt sollen inverse Probleme, wie sie bei rheologischen Experimenten auf verschiedenen Skalen auftreten, formuliert, analysiert und gelöst werden. Insbesondere betrachten wir Actomyosin-Tropfen, bei denen die Interaktion der beteiligten Proteine einen Fluss innerhalb des Tropfens erzeugt, aus dessen Beobachtung wir Rückschlüsse auf die Eigenschaften dieser aktiven Materie ziehen wollen, insbesondere auf die Viskosität, aktive Kräfte sowie Eigenschaften des Actomyosin-Netzwerks.

Forschung allgemein:

  • Nichtlineare und zeitabhängige inverse Probleme:
    • Analyse und Regularisierung
    • Beispiele: Terahertz-Tomographie, Bestimmung von Materialparametern (z.B. Brechungsindex, Viskosität)
  • Einsatz von maschinellem Lernen bei der Lösung inverser Probleme:
    • Post-processing in der Computertomographie
    • teilweise erlernte Lösungsverfahren
  • Parameteridentifikation für partielle Differentialgleichungen:
    • Analyse von Parameteridentifikationsproblemen
    • Beispiele: Bestimmung von Viskosität und aktiven Kraftdichten in der Stokes-Gleichung (Zellphysik)
  • Tomographische Bildgebung:
    • Terahertz-Tomographie
    • Computertomographie (CT), insbesondere Nano-CT
    • Magnetpartikelbildgebung
  • Regularisierungsverfahren:
    • Stabile Lösung inverser Probleme bei verrauschten Daten
    • Beispiel: sequentielle Unterraum-Optimierung
    • Kombination mit deep learning (hybride Verfahren)
  • Inverse Probleme mit ungenauem Vorwärtsoperator:
    • Kompensation von Modellfehlern bei der Regularisierung
    • Anschätzung von Ungenauigkeiten
    • insbesondere: zeitabhängige Fehler im Modell